| 技術名稱 | 結構體解析方法、電腦程式產品與裝置 | ||
|---|---|---|---|
| 計畫單位 | 國立中央大學 | ||
| 計畫主持人 | 李姿瑩 | ||
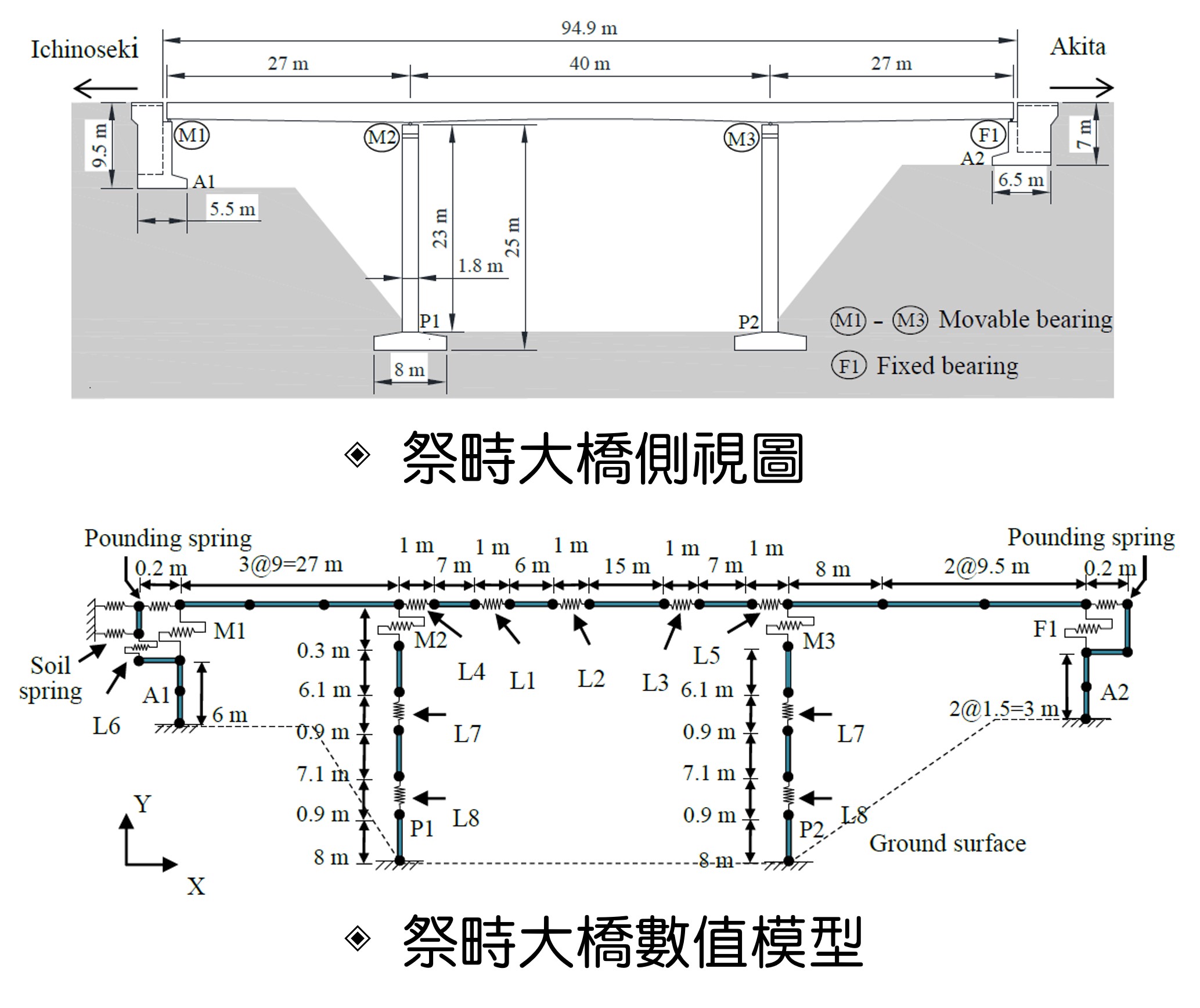
| 技術簡介 | 傳統結構動力有限元素分析採用隱式直接積分法進行非線性歷時分析之主要缺點為結構特性矩陣之反矩陣計算,非常耗時且容易發散。目前工程界與學術界進行非線性動力歷時分析時,經常採用顯式直接積分法,其優點在於不須解反矩陣,但分析大型結構系統時,為避免數值發散,必須採取非常小之時間步幅,因此大幅增加計算時間,反而喪失不須解反矩陣的優點,此外,顯式直接積分法另一缺點為無法考慮勁度阻尼,在僅考量質量阻尼情形下,無法消除數值模型產生之高頻反應,該高頻反應並非真實存在,經常影響分析結果之準確性,因此,目前工程界與學術界對於大型複雜結構之結構動力問題無法精準又有效率地解析。為結合傳統隱式法與顯式法之優點,且未有其缺點,本分析方法提出等效節點割線勁度與阻尼係數之概念,使結構勁度矩陣與勁度阻尼矩陣對角化,並採集中質量方式建立對角化質量矩陣,亦即使運動控制方程式為非耦合,因此不再需要進行矩陣運算,同時可自由選擇任何隱式直接積分法及採用較大之時間步幅,大幅提高計算效率,並且容許模擬結構勁度阻尼,有效避免在反矩陣運算時經常發生之數值發散情形。經由大量之數值驗證,本法之收斂速度等同於傳統迭代程序之收斂速度,數值解的穩定性與正確性等同於傳統隱式直接積分法之穩定性與正確性。由於不需建立結構勁度矩陣與阻尼矩陣,且僅需計算元素之節點內力與阻尼力,任何形式之有限元素與阻尼元件均可簡易地直接加入本分析程序中。因此,本法具有簡易性、穩定性、強健性與高效率等多項特性,可廣泛運用於處理各種非線性與不連續之棘手力學問題。 |
||
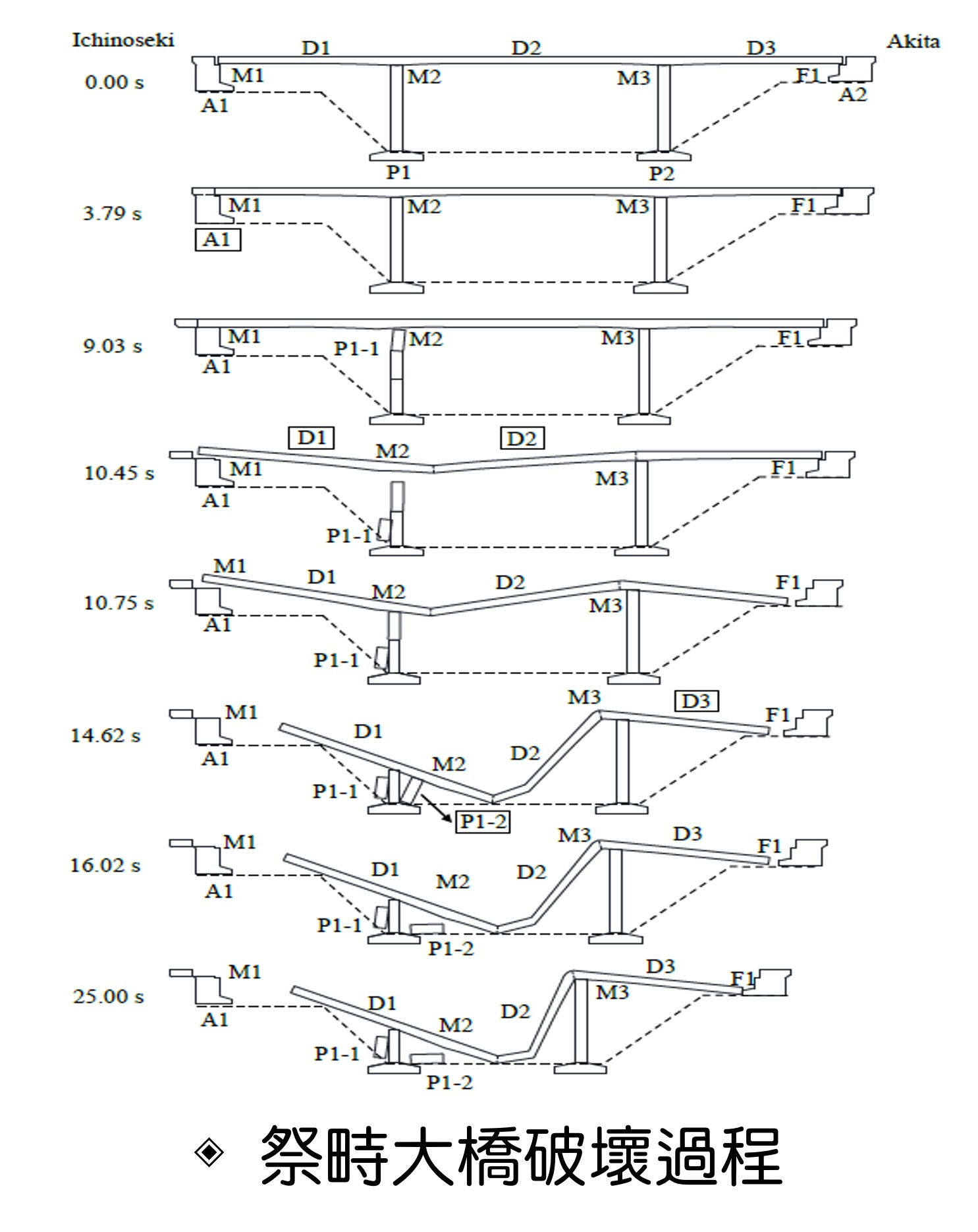
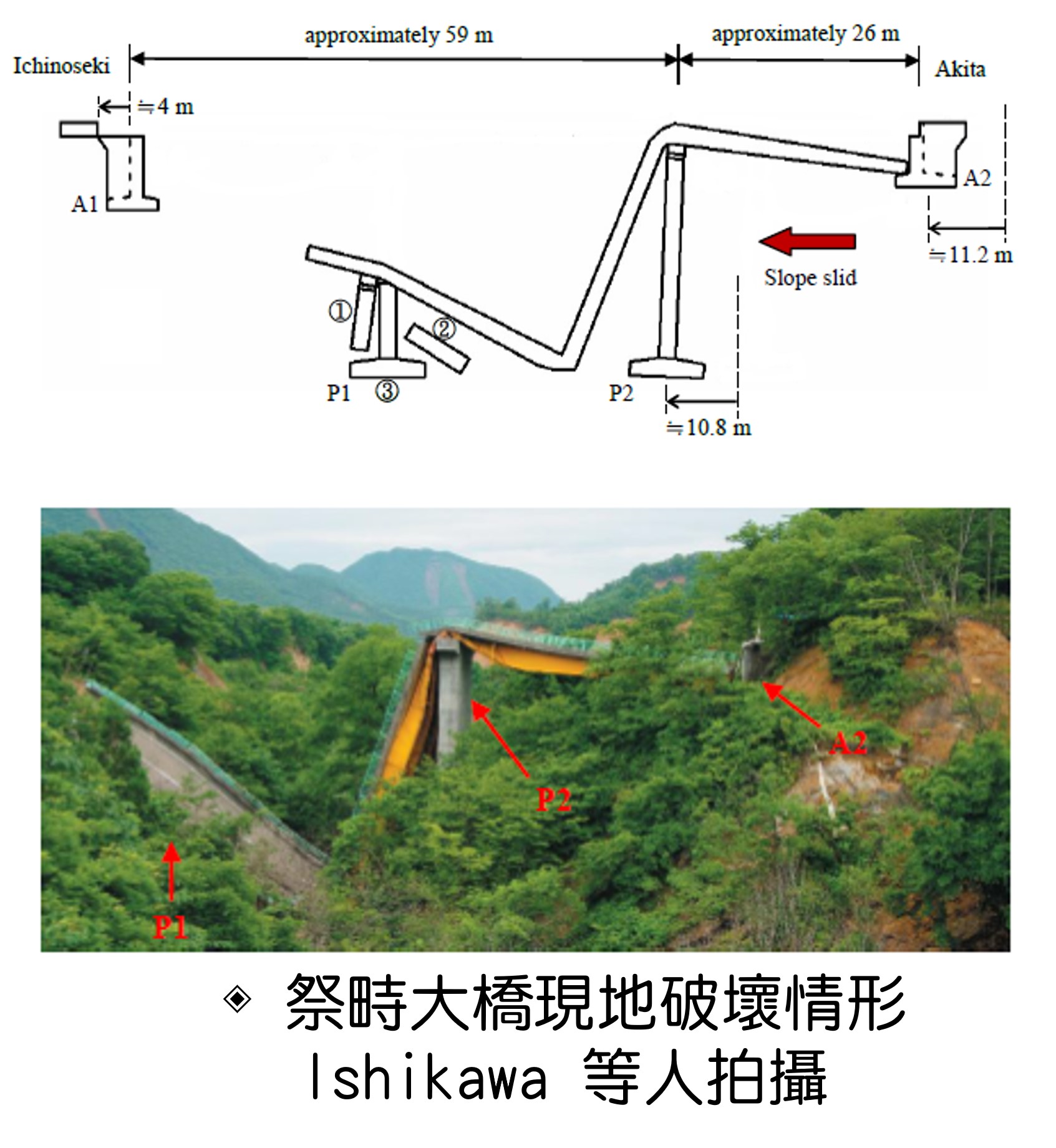
| 科學突破性 | 本法突破傳統隱式法與顯式法各有其優缺點之現況,結合兩方法之優點,且未有其缺點,同時具有簡易性、穩定性、強健性、相容性且高效率等多項特性。目前商用結構分析軟體仍無法模擬高度非線性且不連續之結構破壞崩塌行為,但藉由本分析程序可精準模擬如地震、洪害、暴風、撞擊、爆破等極大外力作用下之結構物破壞崩塌反應。 |
||
| 產業應用性 | 本法可解決目前所有商用結構分析軟體或習知有限元素分析方法皆無法處理之工程難題,同時可用於開發各種新型有限元素,如:結構控制新元件、特殊阻尼元件等,均可簡易、快速、相容於本計算程序。本法可成為工程實務界之一大利器,大幅提升計算效率與降低分析成本,藉以發展未來先進新穎工程技術,實深具產業利用價值與潛力。 |
||
| 關鍵字 | 結構動力 有限元素分析 高效率計算 強健性 相容性 簡易性 新元素開發 新元件開發 非線性與不連續反應 破壞順序與崩坍狀態 | ||
- 聯絡人
- 李姿瑩
- 電子信箱
- tylee@ncu.edu.tw
其他人也看了