| Technical Name | Analysis Method, Computer Product and Device for Discontinuous Structure | ||
|---|---|---|---|
| Project Operator | National Central University | ||
| Project Host | 李姿瑩 | ||
| Summary | Nowadays when analyzing large complicated structures, it requires a much greater amount of computational effort for matrix operators and has some restrictions. An implicit dynamic analysis procedure based on the concept of equivalent nodal secant stiffness and the damping coefficient for diagonalizing the stiffness matrix and stiffness-proportional damping matrix, respectively, was developed. The developed method efficiently and robustly analyzes structures exhibiting highly nonlinear and discontinuous behaviors. Any existing or new finite element and velocity-dependent damping can be directly included in the analyses without numerical difficulty. Additionally, any implicit integration method can be chosen by users. Thus, this method can be extensively adopted to deal with a great variety of nonlinear and/or discontinuous mechanics problems which cannot be solved by the existing methods. |
||
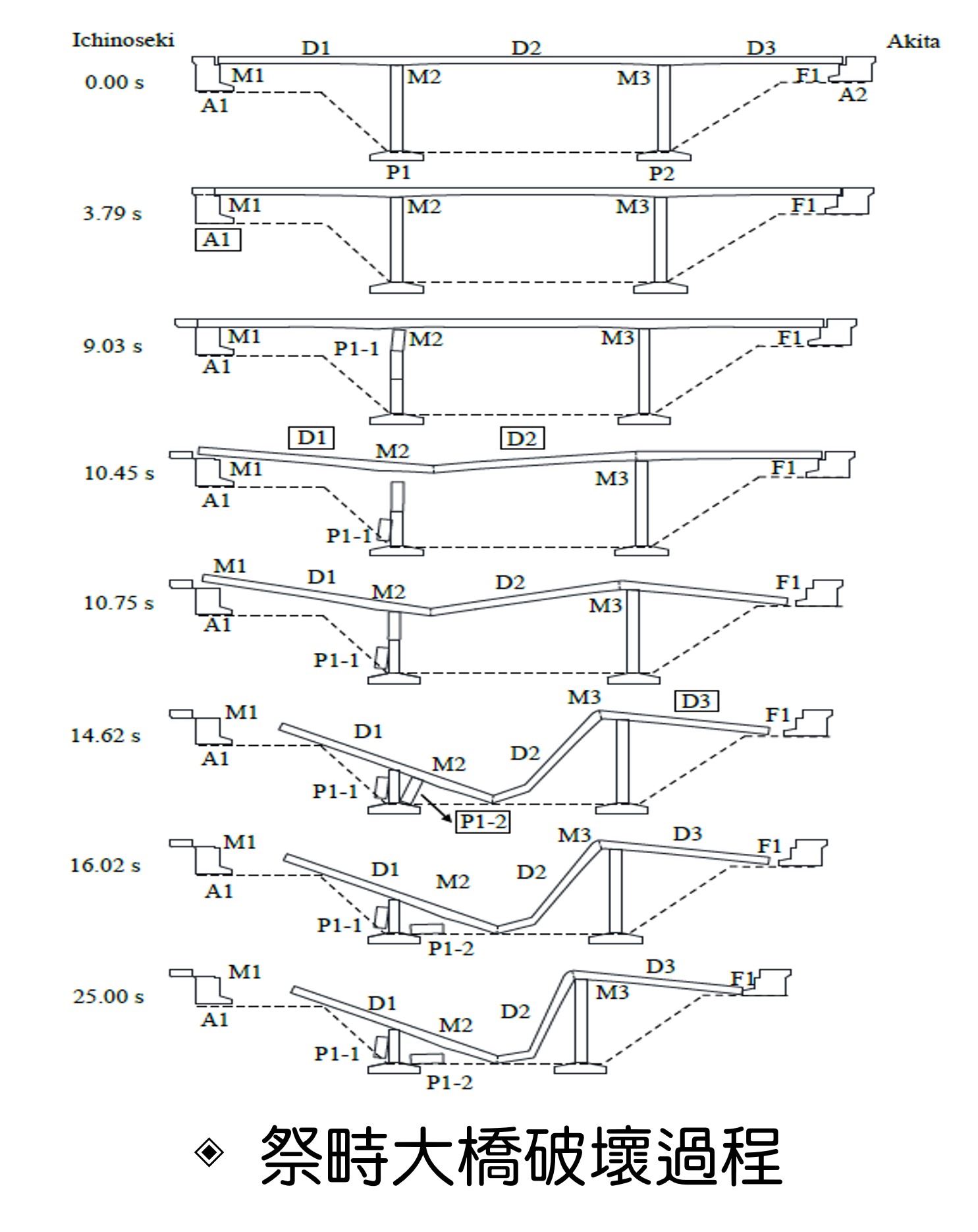
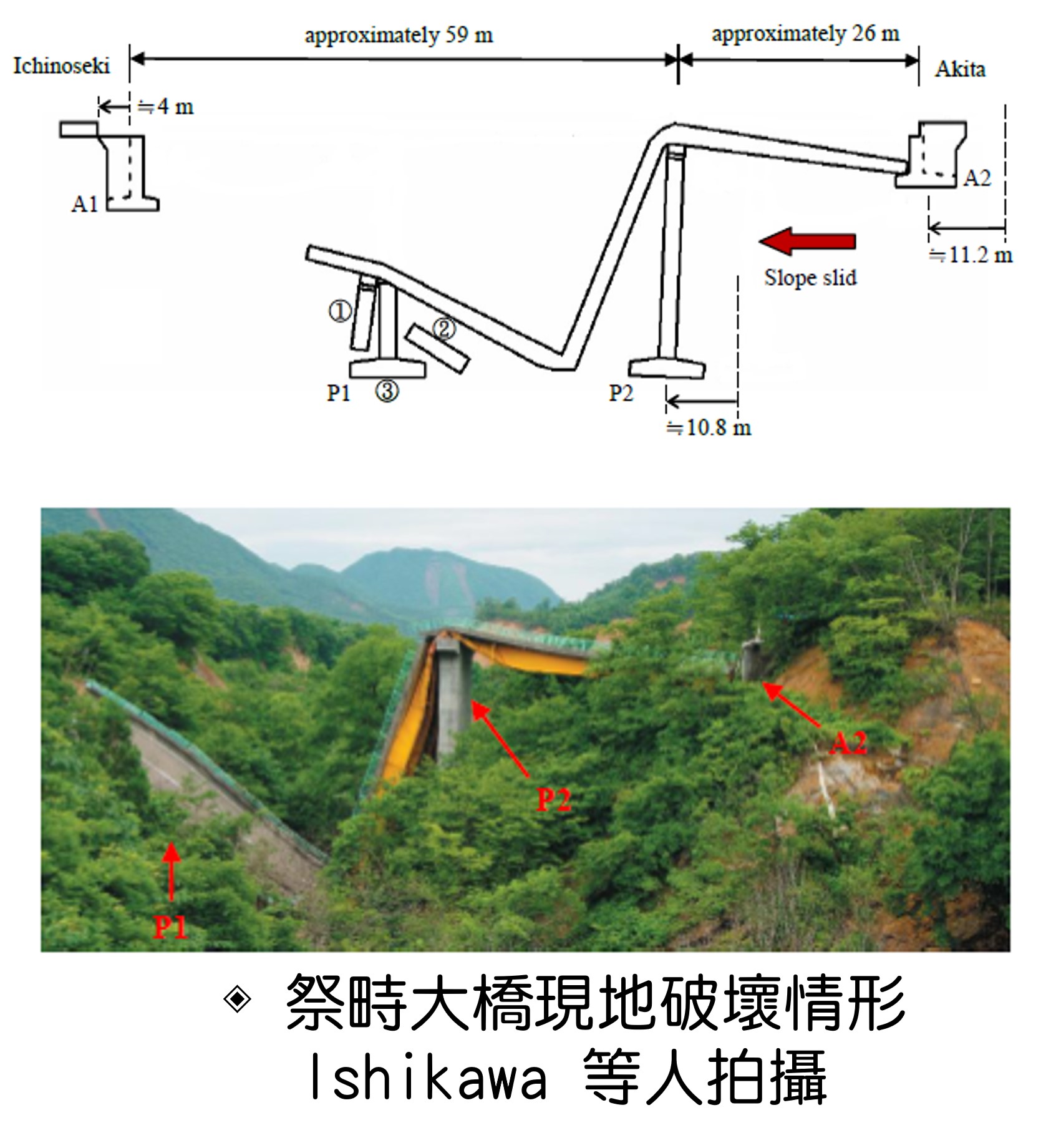
| Scientific Breakthrough | The developed method has the advantages of both the conventional explicit and implicit integration procedures, but with their disadvantages removed. This method possesses the simplicity, stability, robustness, compatibility, and efficiency in nonlinear computations. The existing commercial software is incapable of simulating the highly nonlinear and discontinuous behaviors when a structure undergoes damage and collapse. However, this method can precisely simulate the collapse procedure of the structures under extreme earthquakes, floods, windstorms, collisions, and explosions. |
||
| Industrial Applicability | The developed method can solve the difficult engineering problems which the existing commercial software and well-known finite element analysis method cannot tackle. This method can be adopted to develop a variety of new finite elements, such as new structural control devices and special damping devices, which can be included in this method simply, rapidly, and compatibly. When using this excellent tool in the engineering industry to develop a novel technology, it will dramatically increase the computational efficiency and reduce the cost. Therefore, it is highly valuable and potential to implement this method in industry. |
||
| Keyword | structural dynamics finite element analysis high efficient computation robustness compatibility simplification development of new element development of new device nonlinear and discontinuous response damage procedure and collapse condition | ||
- tylee@ncu.edu.tw
other people also saw